“What I cannot build, I do not understand.” – Richard Feynman
Since I go around pretending that I know how control of the lower urinary tract (LUT) works, surely I can build one. (Not build one out of squishy cells and organs – come on, give me a break – but out of mathematical equations that, when solved, predict where the urine is, what the pressures are, and the rest of the salient LUT states.) Feynman’s idea is that we only understand something well enough if we can build a clear, functioning mathematical model of it, and so much the better if it can predict things.
Well, spoiler alert, the field has been working on this for some time and we really don’t have an acceptable model of how all the component parts of the LUT dynamically work together at the level of organs, urine, pressure, and neural algorithms (i.e., what we call the systems physiology level in the business). As part of my group’s ongoing efforts to solve the LUT modeling problem with an irreverent amalgamation of AI and differential equations (thank you, NIDDK), we are focusing on the simplest possible model that captures the essential features of the LUT in parallel with our attempts at a comprehensive one.
This raises the question, what are the essential features of the LUT? I’m glad you asked.
1) The bladder fills with urine.
2) At some suitable fullness, the LUT coordinates its component parts to void that urine (peeing).
3) Rinse and repeat (1) and (2).
That third feature is key. The LUT exists in a perpetual loop of fill-to-void cycles. Thus, at the bare minimum, any solution to a system of differential equations we use to model the LUT must have cyclical solutions (i.e., solutions that repeat themselves in time, called limit cycles).
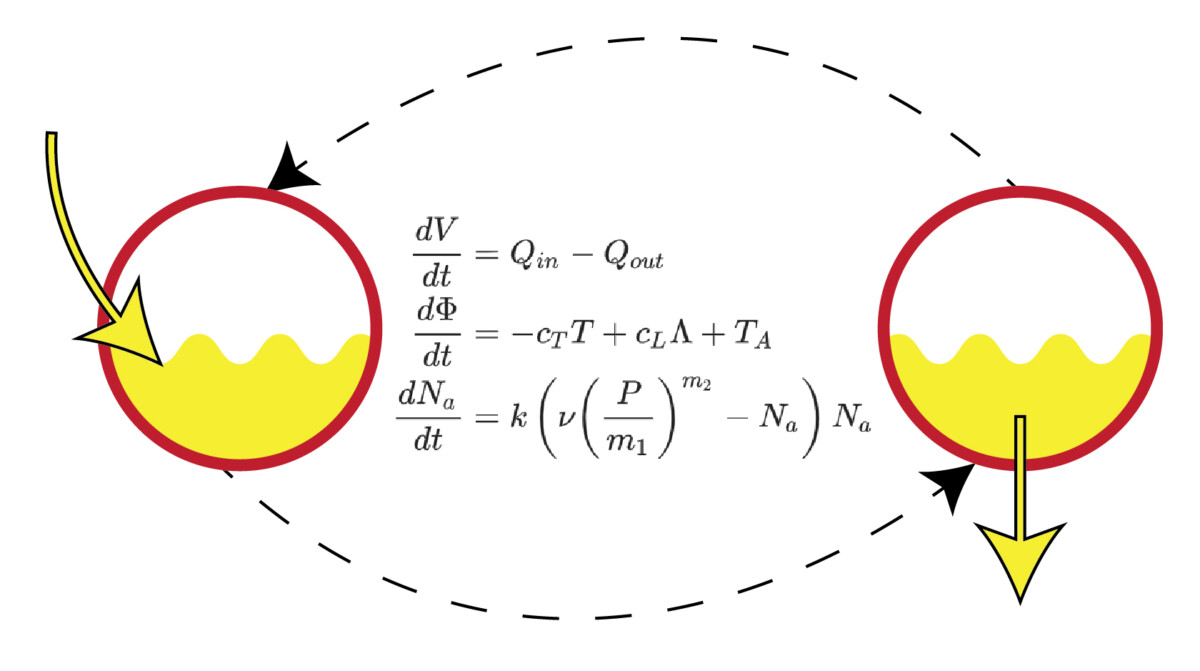
In our new work we present what is probably the simplest possible, yet still plausible, differential equation model of the LUT that generates fill-to-void cycles. The model has three dynamic states (physiological quantities), bladder volume, bladder tension, and bladder sensation (sensory neuron discharge). Although we have simple expressions (and beautiful clip art) for many other physiological quantities (like pressure, bladder radius, elasticity, etc.), only the 3 brown underlined states (figure below) are modeled dynamically, yielding a 3-equation system.
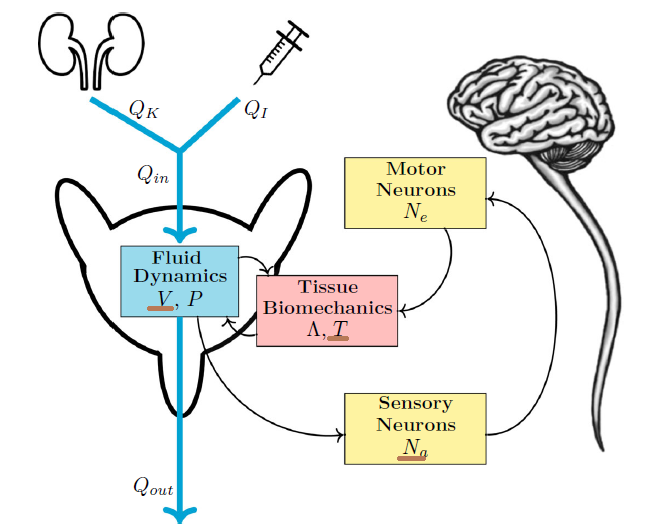
We abstracted away a great deal here (including fan-favorites like the urethra and the brain), but the point is not realism, it is to see what basic ingredients are strictly required to get the 3 essential features of LUT behavior: fill, void, repeat. Looking at what the austere model predicts, compared to what we record from the rat (figure below), we see the essential cyclic behavior we were looking for. Importantly, we didn’t demand the model generate limit cycles, we gave it a few simple things we knew about the LUT (urine cannot be destroyed by the bladder, tension develops in the bladder only once it has uncrumpled, etc.) and cycles emerged spontaneously.
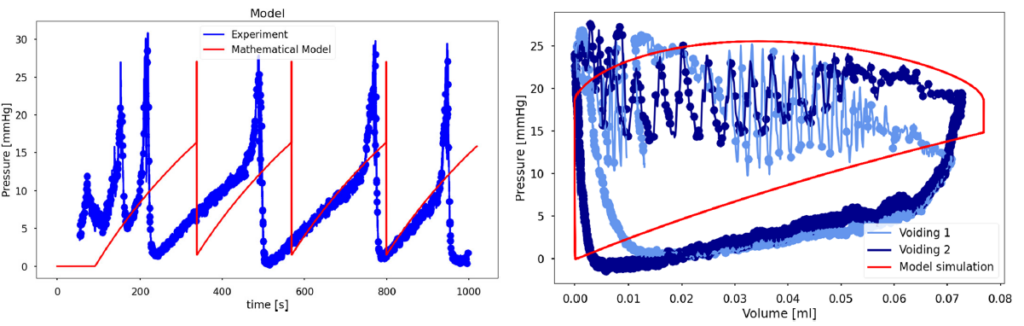
Although the model’s bladder isn’t squishy enough (notice the higher filling pressure than the experiment at the same volume – right) and it voids too quickly (notice the narrower pressure peaks in time than the experiment – left), it captures the general fill-void-repeat behavior with surprisingly few equations. Our ongoing work is focused much more on accuracy using obscenely complicated equations that are much harder to analyze and understand. The benefit of this relative simplicity model is that we understand much more about what is going on. For example, how much can we mess with the model before we lose the limit cycles?
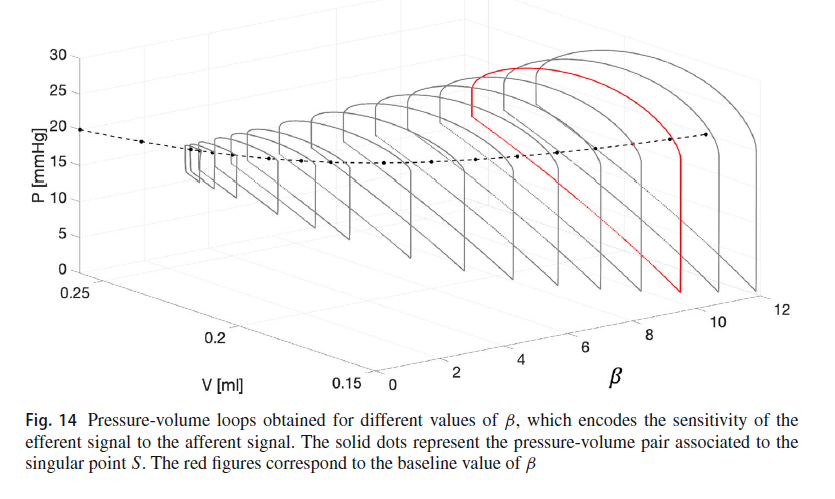
Dr. Nunez explored just that. In the figure above, the loops around pressure and volume created by the fill-void-repeat cycles are 2D slices in the overall abstract 3D space. The extra dimension is “beta”, a parameter in the model. The more beta you have, the more intense the neural “contract the bladder” command is for the same amount of bladder fullness sensation. In other words, the larger the beta the more vigorously the nervous system contracts the bladder in response to filling. As beta gets low the cycles shrink in size, corresponding to weaker and less efficient voiding. Eventually the cycles are destroyed, and the urine just leaks out of the bladder – a simple model of overflow incontinence – the bladder is essentially flaccid without a strong enough incoming command to get a robust contraction.
With a simple and robust model like this, we can now test hypotheses about general systems-level function in broad strokes much more easily. Although my first love is the urethra, this model predicts that even replacing it with a simple collapsible tube you would still see the essential fill-void-repeat behavior. I’m not suggesting we should start replacing people’s urethras (voiding would become terribly inefficient), only that the model shows to maintain this aspect of LUT behavior (cycles) the urethra isn’t strictly necessary. These ideas will help guide us about which organs and tissues, when dynamically linked, give rise to which behaviors. The future holds exciting simulations.
Nunez R, Alhajjar E, Jaskowak D, Danziger ZC, Giodoboni G, “Onset of Spontaneous Filling and Voiding Cycles in the Lower Urinary Tract: A Modeling Study.” Bulletin of Mathematical Biology, 86:122 2024.
doi: https://doi.org/10.1007/s11538-024-01320-1