Imagine, if you would, a future where your favorite local urologist could tell you how many milliliters your bladder will void two years from now (given the details of your crappy diet and current weight) with the same precision that your favorite local astronomer could tell you where Venus will be in the night sky two years from now (given its current position and velocity). Such a prediction requires more than a theory – it requires a mathematization of our knowledge. Physics gifted humanity with a theory of motion that tells us that planets orbit the sun, but it’s the mathematical language of the theory that tells us precisely where the planets will be (within limits). Mathematizing our theories of the urinary tract would manifest incisive predictive power to the delight of urologists and patients everywhere. It would revolutionize diagnostics in urology. This goal has motivated many scientists to attempt a mathematical description of the urinary tract, and it is the partial successes of those attempts that motivated my research group to outline a field-wide plan for a more complete model.
When done well a mathematical model does more than predict, it can generate causal hypotheses. It grants you the power to remake reality like a god in whatever part of the world the mathematical model is valid. This control is the core of causal analysis, made possible by counterfactual reasoning. What would the orbit of Venus look like if Planet X were to exist? When theories aren’t mathematical, the best we can do is use them to help us reason through the implications of what would happen if we changed x, y, or z (which can sometimes lead to strange places, or worse, actually creating an infinite number of strange places). With a mathematical model, on the other hand, we can actually instantiate the change to the world we are speculating about by updating the model equations or parameters; solving (i.e., simulating) the updated model tells us precisely what would happen if the change had occurred in the real world. A urinary tract model would let us generate hypotheses about so many currently mysterious processes through endless tweaks to its parameters, and make focusing work on developing new treatments much sharper. Accurate prediction and counterfactual reasoning are the shimmering jewels rigorous mathematical modeling affords.
How does it work now? More or less, the current strategy is for a small, ambitious team of scientists to codify mathematically what they know about the lower urinary tract. Bits and pieces of their models are borrowed or refactored from earlier works, with the bulk of the effort dedicated to mathematizing the parts the team is most interested/fixated on. The team’s model is then published, hopefully with a careful description of the math and a few images of what the model predicted. This has led to some successes, for example, predicting bladder pressure from nerve stimulation, extracting patient-relevant physiological parameters from clinical diagnostics, qualitatively altered dynamics from neurological injury, or quantitative analysis of abstract requirements for stable fill and void cycles.
The problem with this approach, though, is that each of these models can make narrow predictions in their domain of validity but lack predictive and/or counterfactual power in other important regions. Unfortunately, the lower urinary tract really is more than the sum of its parts. When the goal is to understand how a disease or treatment impacts urinary health (i.e., function), one really must know how the effects of a change propagates through the entire system. This is true, in part, because of the complex reflex control that coordinates the muscles throughout the urinary tract and in part because of the details of the mechanical coupling between its physical structures.
There is just too much in the urinary tract to keep track of. And if we are too off with the mathematics of even one part, that error will propagate through all the interactions in the model and lead to inaccurate predictions. We put together a list of the most critical parts (circle segments) and how they relate to one another (lines) that we think we need to have a mathematical description “complete enough” to make accurate predictions. It’s in the figure below. It paints a grim picture of so many parts and connections that it doesn’t seem possible for one team to tackle it all.
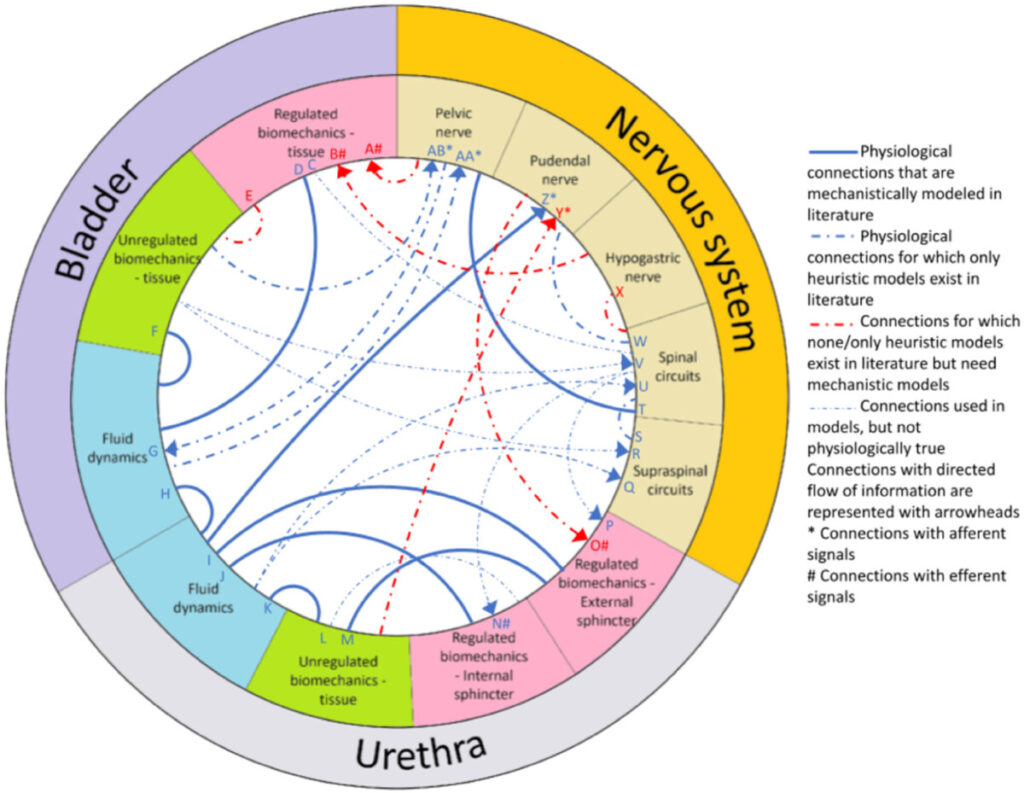
How can we make progress? There’s no simple solution, but there is a possible way forward. If the full system is too complicated for a single team to tackle in a timescale of a typical research project, then we should stop trying to build the model that way. Instead of full models, teams could focus their energy on building out the mathematics of one component of the urinary tract – perhaps the one they are most familiar with or have enough experimental data on which to base their models (e.g., one branch of one nerve). If a) teams build individual components in parallel, b) follow credible practices for model development that let others understand and reproduce the work, and c) and keep the scope of their models at the same spatial scale (i.e., the level of tissues, organs, and fluids, rather than cells or cognition), we could put the individual component models together like building blocks to form the whole. If each component mathematical model were constructed with modularity, interoperability, and extensibility as design requirements, the field could build the full model one brick at a time. This allows each team’s strengths to shine in constructing the parts they are best suited to design, rather than asking each team to know a little about all the components.
Getting the final full model wouldn’t be anything close to as simple as just sticking all the component models together, since all sorts of parameters would need to be retuned and their interactions validated, but that could be the purview of yet another team with the appropriate expertise. The larger effort would require explicit collaboration among the modeling community to get over the collective action hump; each team would need to agree on the level of explanation to target and build their models to connect with that level (either by building models at the tissue level directly or by making an information bridge where state variables representing bulk properties could pass from lower level models to the tissue level). For a component model to contribute to the larger effort its authors would need to explain which of its state variables interact with which other components (even if no models yet exist for those components). Divide an conquer, but where each battle won is targeted at a missing part of the larger whole, and together we can have accurate prediction and quantitative counterfactual reasoning for systems urology.
Jaskowak D, Nunez R, Ramachandran R, Alhajjar E, Yin J, Guidoboni G, Danziger ZC (2022). “Mathematical modeling of the lower urinary tract: A review.” Neurourology and Urodynamics 41(6):1305-1315.