A powerful technique for generating insights into physiology is to mathematically express what we know about it, then to simulate it in a computer. With the mathematical expressions in hand you can change whatever part(s) of the system you’re interested in and see in silico how that reverberates throughout the rest of the physiology, shortcutting the painstaking laboratory studies that would otherwise be required to satisfy those curiosities. I’ve touted the merits of this approach before for generating knowledge and for translating that knowledge into treatments, as well as given some examples of how to do it for the lower urinary tract. Raw compute combined with mathematized knowledge of biophysics is without rival in its incisive capacity to puncture the mysteries of how physiology works.
But there is a huge problem: for the computer to simulate the physiology we’re interested in every constituent part of the system needs its own accurate mathematical expression. That is, every organ or tissue that is relevant for our system needs its own hard-won mathematical equation. If the model is missing even one equation nothing will run; an elegant clockwork mechanism with a single missing gear that never tells the time. We can often express simple systems mathematically in their entirety, but most physiological systems are complex and we don’t normally have all the equations because there are parts of the biology (or interactions between its parts) that we don’t understand. Simulation is off the table.
At this point, it is in vogue to throw AI at the problem. Couldn’t we just let an artificial neural network (ANN) learn the model? First, that’s not what ANNs are good at. They are much better at classifying tons of examples of things or making statistical guesses about patterns than inventing mathematical descriptions of reality from whole cloth. Second, ANNs need lots of data to learn, which isn’t usually available in systems physiology. Third, and perhaps most importantly, once an ANN has learned to make good guesses about your problem it is in absolutely no mood to explain to you how it makes those guesses or how its equations map on to physiologically identifiable parts your system (don’t @ me, bro). This undermines the whole idea behind doing mechanistic modeling in the first place, which is to be able to tweak specific parts of the physiology you’re curious about and see how the rest of the system responds.
We (the research team I work with) proposed a new approach to get around incomplete models where we hold onto all the mathematical descriptions of the physiological parts we are confident about and just wedge small ANNs into slots where we are missing the equations. This (if it works) solves so many of the traditional problems in computational modeling of systems physiology. 1) We can simulate physiological systems even when we’re missing some equations. 2) We don’t need much data, since the ANNs we have to train only occupy a small percentage of the total system. 3) The model is still interpretable everywhere we have traditional mathematical expressions, which (usually) forces the ANNs to at least have physiologically meaningful outputs, even if their expressions don’t have clear physiological interpretations.
In our new work, we developed a method for training these hybrid biophysical-ANN systems and show that ANNs embedded among biophysical (ordinary differential) equations learn to approximate the output of missing equations. That is, with our method the stop-gap ANNs learn to generate missing (unmodeled and unmeasured) physiological states, letting us computationally simulate a physiological system even when we don’t know all its equations. A sample of the results are in the figure below.
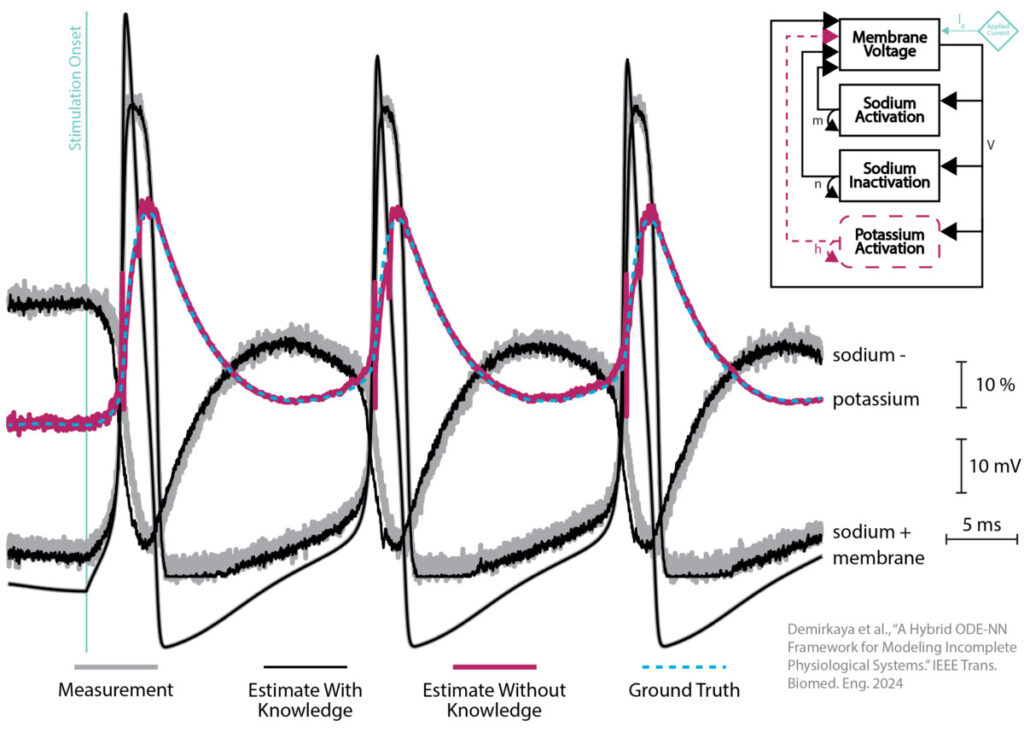
We show a couple of validating examples, one being the famous Hodgkin-Huxley neuron model. The HH model has four equations, one for the cell membrane voltage and three more for different pore dynamics that let ions into and out of the cell. The inset shows that we provide our framework with three out of four equations (black rectangles) and substitute an ANN for the fourth (dashed maroon oval). We provide the training framework measurements (gray traces) for the signals corresponding to the parts we know (black rectangles) and the hybrid model, unsurprisingly, can accurately simulate them (black traces). The big reveal is that the ANN learns to accurately generate the fourth signal (maroon trace) even though we do not provide it with a measurement of that signal (blue dashed trace) or information about the equation that should be generating that signal. We are very excited about this result (and similar results on models of ocular circulation) because it means we will be able to use this approach to simulate a variety of physiological systems for which we have incomplete knowledge and measurements.
The nuts and bolts of how we train these hybrid models of ANNs embedded in standard systems of ODEs is by using Kalman filters. We formulate the training problem as recursive Bayesian state estimation, treat the to-be-learned ANN weights just as though there were extra physiological states to be estimated (with non-dynamic state transition but high covariance estimates), write the ODEs as part of the filter’s state transition model, then infer the combined weights and physiological states at each timestep. Slowly, the ANN weights converge (learning!) and start to accurately output the missing physiological state while the known mathematics of the other ODEs (that constrain the ANN output because it is an input to the ODEs) output the measured states.
Now that we have a way to train such hybrid (ANN-ODE) models, I hope they can be useful wherever we need simulations but have incomplete knowledge – which is pretty much everywhere with systems physiology.
Demirkaya A*, Lockwood K*, Imbiriba T, Stratis G, Ilies I, Rampersad S, Alhajjar E, Guidoboni G, Danziger ZC†, Erdo˘gmus D†, “Biological System State Estimation Using Cubature Kalman Filter and Neural Networks.” IEEE Trans. Biomed. Eng., 2024 (*:co-first author, †:co-last author)
Ghanem P, Demirkaya A, Imbiriba T, Ramezani A, Danziger Z, Erdogmus D, “Learning Physics Informed Neural ODEs With Partial Measurements.” AAAI 2025 (or on arXiv)
