TOC graphic from Ziwei and Peiyao’s paper in Soft Matter

In collaboration with the Weeks group in the Emory Physics Department, we are studying the ordering transition of monolayers of colloidal silica particles settled from aqueous suspension onto a glass surface.  Starting over the summer of 2017, Yijun Dong (Emory College, class of 2018) and Peiyao Wu (Emory College, class of 2020) have been working towards measuring how large (and heavy) these particles need to be to settle into a hexagonally ordered monolayer.

The image below epitomizes the collaboration – the circles represent particles imaged in Yijun’s experiments, while the color coding (where intensity of color represents degree of local hexagonal ordering and hue represents its orientation) comes from an analysis performed by Peiyao on her simulations.

Kindt group graduate student Ziwei Guo has joined the effort.  A major contributing factor towards the rate of ordering is the nature of the interface between domains of similar order.  The interface is known as a “grain boundary”.  Ziwei has used Monte Carlo simulation to calculate how the stiffness of a grain boundary in a polycrystalline hard sphere monolayers depends on the mismatch in the angles of the lattices of the two grains.  (See here or here (pdf).) He has also studied how impurities (hard spheres with a different size) partition between the interiors of the grains and the boundaries, and found that a specific size of impurity shows qualitatively distinct patterns of preference in the types of grain boundaries it prefers.  We propose that this size of impurity is just the right size to substitute in for pentagon-shaped sites at the grain boundary (shown in the picture below) associated with dislocations, whose presence is strongly dependent on the relative orientation of the two grains (accepted for publication in Langmuir).

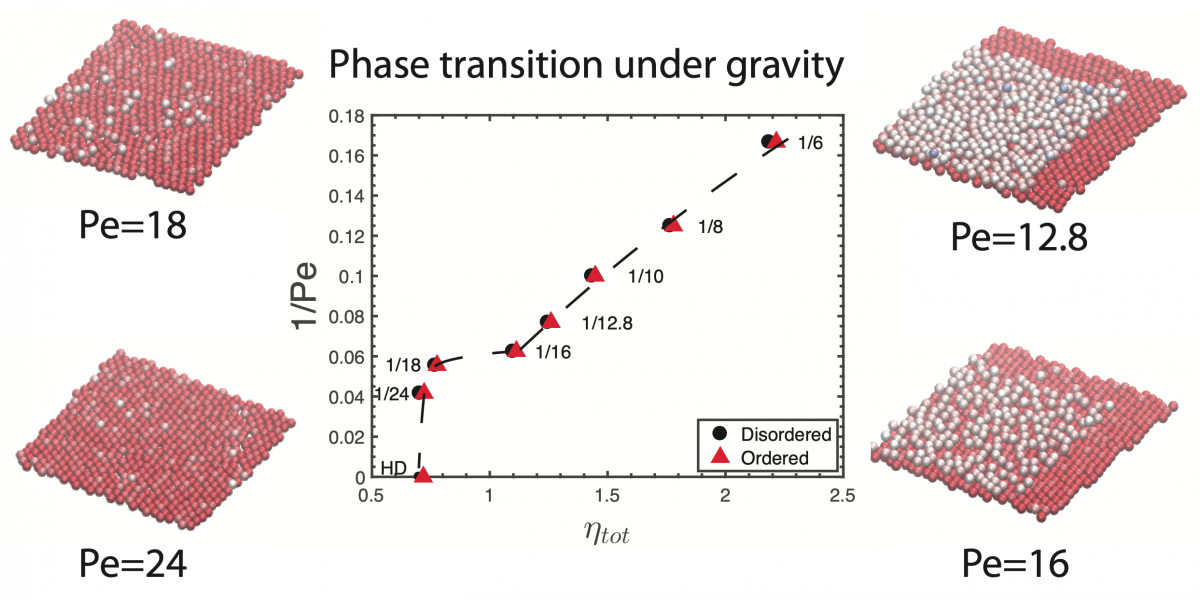
Ziwei’s analysis of grain boundary effects and Peiyao’s simulations of phase behavior in the quasi-2d system of hard spheres under a gravitational potential have been published in Soft Matter; a preprint version is available here and the official version on the journal website is here.