To assess bladder health we need to know (among other things) how well it can empty. We quantify this via the voiding efficiency (VE), which is the fraction of urine in the bladder that actually gets pushed out (the brave can follow my more detailed treatment of voiding efficiency and its measurement in another post). Speaking cavemanatically (100% a real word), high VE good, low VE bad. We compute VE as the volume voided divided by volume voided plus the residual volume left in the bladder (which should be all the volume available to void). Mathematically, VE = Vv / (Vv + Vr).
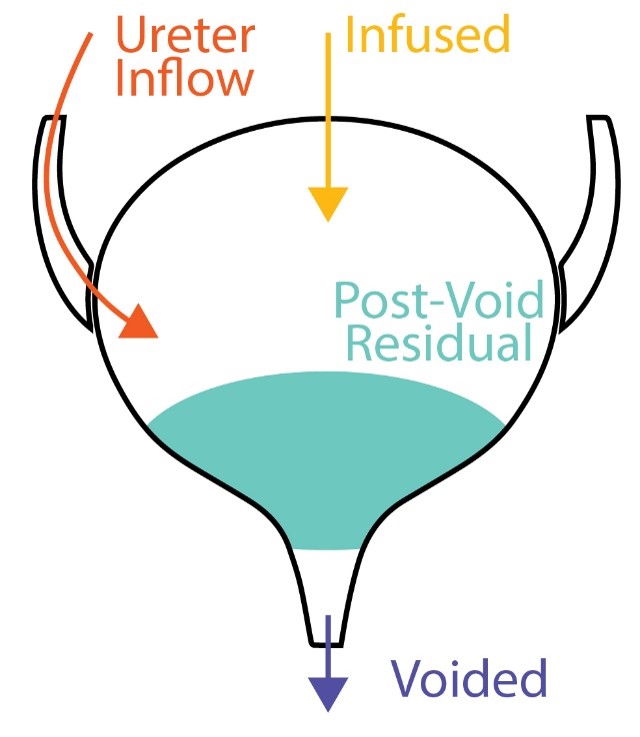
But should we trust the measurements from which we compute VE (voided and residual, i.e. Vv and Vr)? The voided and residual volumes can be tricky to measure accurately, which in turn, could corrupt our VE calculation.
Consider the diagram (left) that implies “volume into the bladder is equal to volume out plus the residual”. This brings into view that all volume available for voiding is equal to all the volume put into the bladder during filling. There are two sources of filling, infused volume by the experimenter (Vi) and natural filling by the ureters (Vu), only one way out (Vv), and everything left must be the residual (Vr):
Since we know Vi (we set the rate on the infusion pump, after all) and measure Vv and Vr, through the magic of algebra we can calculate the missing variable in the equation above, Vu, the natural ureter filling.
\(V_u = V_v + V_r – V_i\)Here is the simple proposal: if the Vu we compute is negative (or egregiously large) then we have made a mistake. That’s the whole idea. Since we can’t have a negative volume (well, a physicist can’t but an economist can basically do anything), and we agree that the bladder cannot create or destroy urine, then the only remaining possibility is that we have a bad measurement that led us to compute an impossible Vu. In other words, if Vi is known and Vv and Vr were measured accurately, we couldn’t possibly have a negative Vu; therefore, “when you have eliminated the impossible, whatever remains, however improbable, must be the truth.” The improbable truth in this case is that you should be dubious about your measurements for of this cystometric cycle.
The figure (right) shows this in a simulation of a gazillion cystometry cycles. The blue histogram shows the distribution of actual ureter inflow rate while the red one shows what we’d estimate given measurements of Vv and Vi. The bounding lines show that often we calculate negative flowrates (and therefore volumes) due to measurement noise/error. We can flag those as trials to potentially throw out, making our VE estimates more accurate.
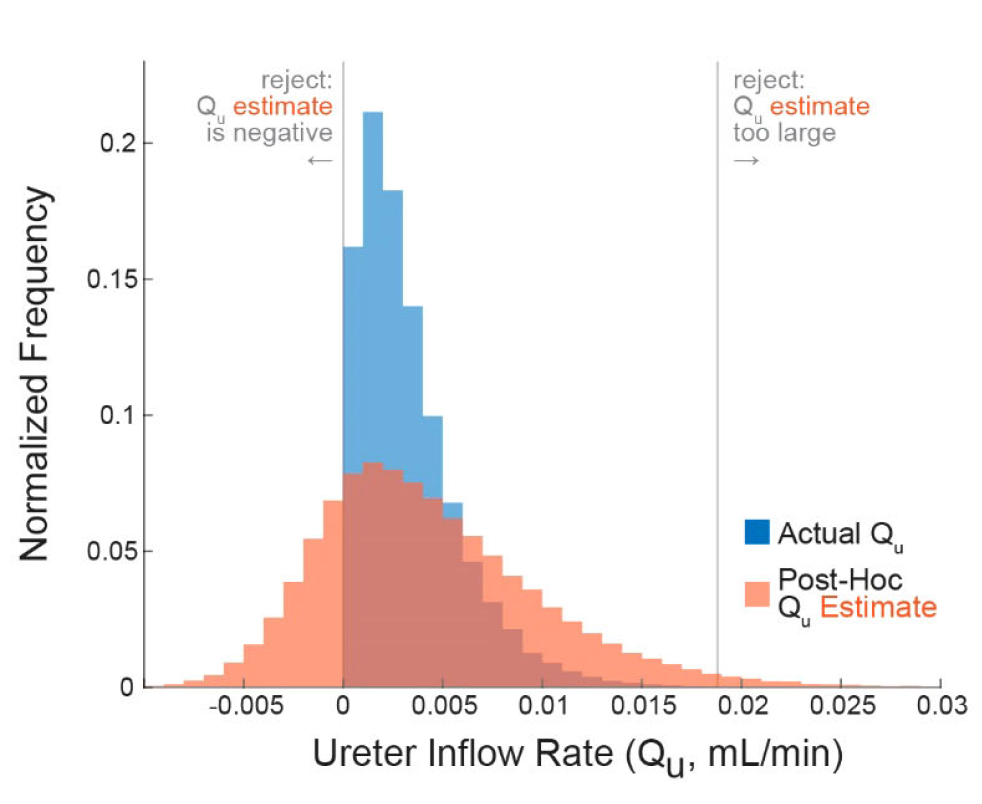
We can all use this negative volume criterion as a way to check our confidence in what we measure and report. In my experience, especially at large infusion rates, many cystometry cycles can have such error. For the full story, check out Frontiers Urology. Happy filling.
Danziger, Z. C. and D. Jaskowak (2024). “On variability and detecting unreliable measurements in animal cystometry.” Frontiers in Urology 4.
Download the simulation code used in the paper. (https://doi.org/10.3389/fruro.2024.1348002)
