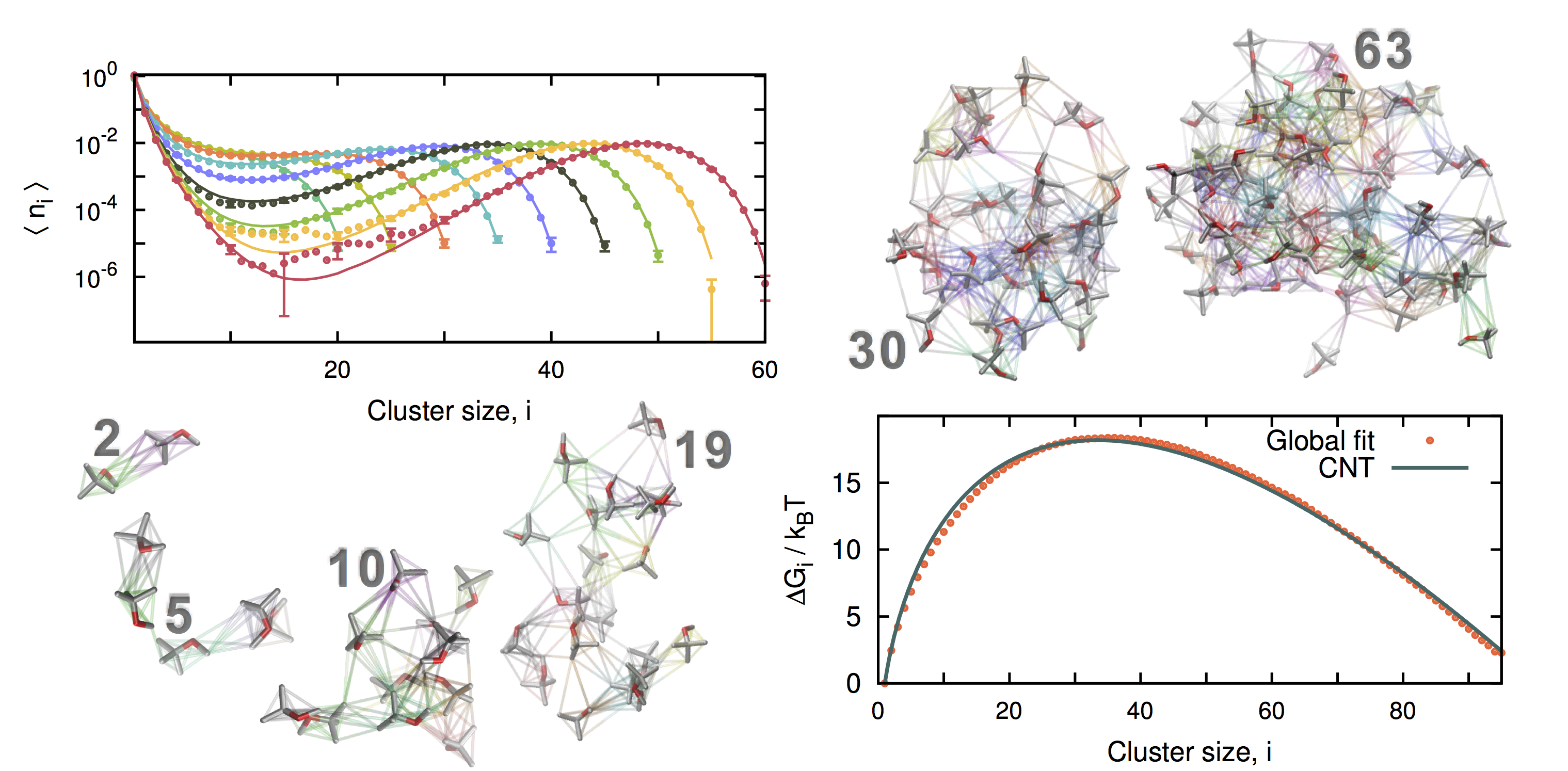
PEACH method: “Small-N” simulations for cluster free energies
The reversible association of molecules into clusters (e.g. nanodroplets or micelles) is an important phenomenon in chemistry and biology. We have been developing ways to analyze the data obtained from simulations of a small number (N) of associating molecules to get at the equilibrium constants for association in the limit of large N. For more details please see here (Physics Procedia article) and here (JCTC article). Starting in 2016, we have been working on these methods in collaboration with Olivia Beckwith and Robert Schneider from the number theory group at Emory’s Department of Mathematics and Computer Science. We have applied these methods to simulations of the formation of liquid nanodroplets of methyl t-butyl ether from both the vapor and aqueous phases, to the formation of small NaCl clusters from aqueous and methanol solution (results published here), and to both neutral and ionic micelle-forming surfactants (here). We have come up with an acronym for our method: Partition-Enabled Analysis of Cluster Histograms, or “PEACH”. The tools allow us to address fundamental questions about how many reacting molecules need to be present for the Law of Mass Action (which is based on an assumption of large-number statistics) and to devise simple, approximate corrections that could help bridge the gap between small-N and large-N statistics.
TOC graphic from Lara Patel’s paper on MTBE
We are applying these methods in united-atom simulations of surfactants (both neutral and ionic) and simulations of surfactant-peptide interactions.
TOC graphic from Xiaokun and Jorge’s paper on octyl phosphocholine
More information on a collaboration with the Bester-Rogac group at the University of Ljubljana is here.
Snapshot of a partially folded peptide embedded in an octyl phosphocholine micelle, work by Jorge Arce.
Methodological extensions that we are targeting include careful analysis of non-ideal effects and a hybrid PEACH-Bennett Acceptance Ratio (BAR) method for slowly exchanging clusters.
Grand Canonical Monte Carlo for Condensed Phases
From Ziwei’s paper in Langmuir
Monte Carlo simulations in the grand canonical ensemble are performed with a variable number of particles of one or more type. Trial moves performed over the course of the simulation generate new structures in which one or more particles are added, removed, or exchanged for particles of a different type. The probability for accepting one of these trial moves depends both on the resulting change in the system’s potential energy (as in canonical MC) and on the chemical potentials (represented by the symbol µ) of all particles involved.
There are a few reasons why grand canonical Monte Carlo (GCMC) simulations can be a useful alternative to simulations that fix the number of particles. One reason is that one learns how µ depends on the system density and composition. This is particularly useful when simulating a system whose composition is determined by exchange of particles with a reservoir – for instance, molecules sticking to a surface or embedded in pores, where the surface coverage or pore loading is dictated by the concentration of molecules in the gas or solution above the surface or in contact with the pores. A discontinuity in composition with changing µ is also a useful indication of a first-order phase transition. Another reason is that exchanging particles with the imaginary reservoir leads to equilibration of composition across all of the microenvironments in the system being studied, and in some cases this equilibration is more efficient than the equilibration that happens through particles diffusing across the system.
Conventional GCMC involves attempts to insert a particle to a random position in the simulation box. In a dense system (for instance, a liquid or solution) these moves are very unlikely to succeed because a randomly chosen position is likely to be occupied by another particle, and the energy cost to add two particles very close to each other is very high. This energy cost can be lower when a particle is exchanged for a particle of a different type (in a “semi-grand canonical” type of simulation), but only if the particles are sufficiently similar in size, shape, and interactions.
Our goal is to develop GCMC methods that allow a particle (and if necessary, its local solvent shell) to be exchanged for a number of solvent molecules. A key challenge for these methods is finding ways to pack solvent into a cavity that are efficient and that satisfy detailed balance. In a “proof of principle” study, Solvent Repacking Monte Carlo was relatively successful for exploring the phase behavior of a 2-dimensional binary hard disk mixture. (See here.) We are working both to apply this method to related systems and understand ordering transitions of hard particles on curved surfaces, and to extend the range of practical applicability. These techniques have been applied to 3-d Lennard-Jones mixtures and to study ordering transitions in colloidal monolayers. Ultimately our goal is to be able to perform GCMC on solutes of moderate size in explicit water.
Snapshot and detail from Solvent Repacking GCMC simulations of a bidisperse hard-disk mixture, with large disks (d=3) shown in white and small disks (d=1) color-coded according to complex value of the S6 order parameter. (Intensity of color correlates to degree of local hexagonal order; hue correlates to the local packing direction.)
Peptide-lipid interactions
We are using MD simulations to study the dynamics of folding and insertion of antimicrobial peptides at lipid bilayers, in collaboration with the Dyer group.
Phase behavior of lipid bilayers
Lipid bilayers undergo phase transitions between ordered (gel or ripple) and disordered (fluid) structures as temperature is varied. Earlier work in the group addressed methods to study demixing effects associated with ordering transitions in bilayer mixtures (here and here), to identify the actual transition temperature of a simulation model (here), and to characterize how lipids are arranged within the gel phase (here). We have been working on several questions related to the structure and properties of bilayers near their transition temperatures:
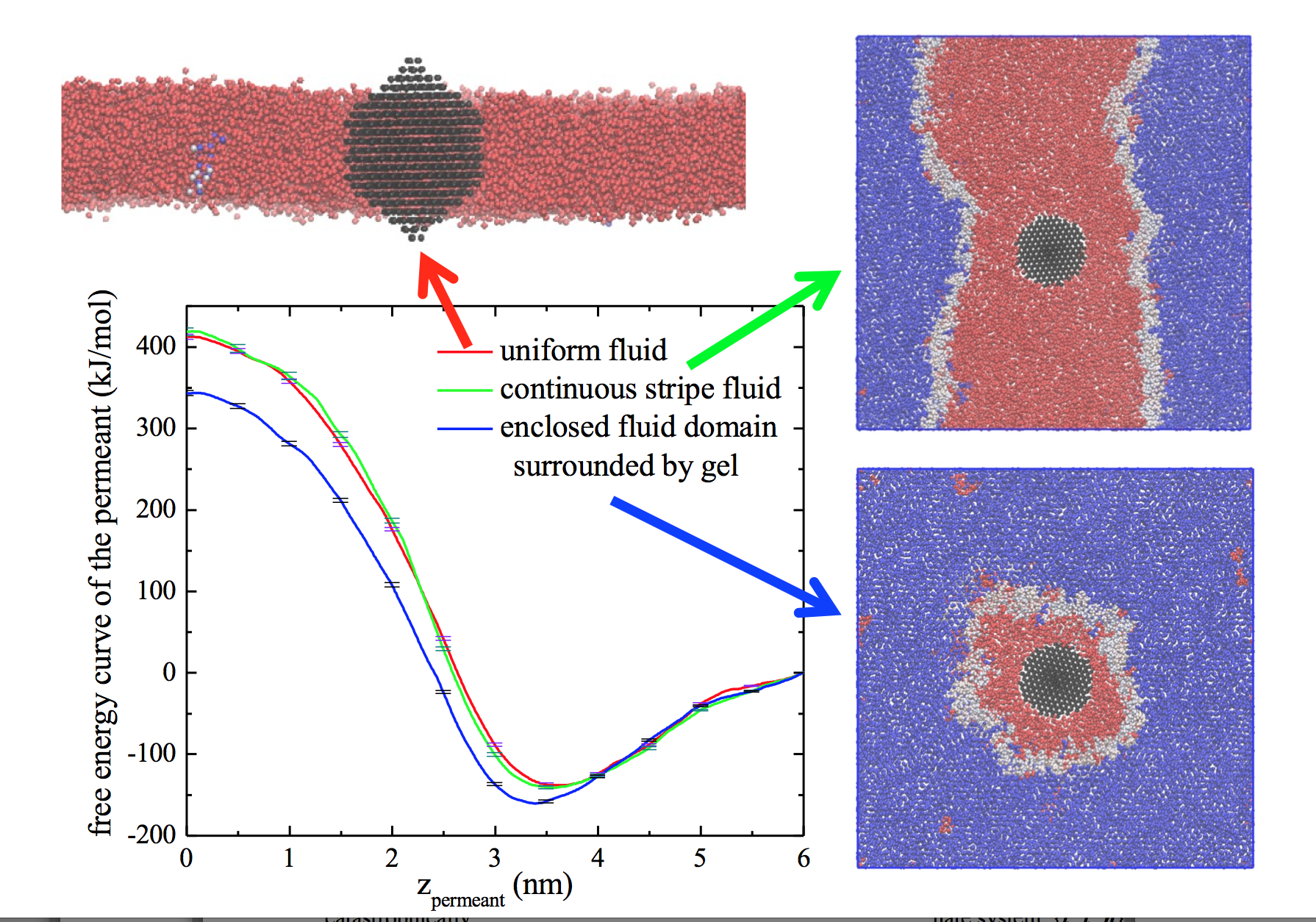
Anomalous permeability. Molecules pass through the bilayer much more easily in the fluid state than in the gel state. Experiments dating back to the early 1970’s have shown that the permeability is greatest near the transition temperature. Lewen Yang has been working on simulations that have helped us develop a new understanding for this anomaly – inserting a molecule into a fluid region that is surrounded by ordered lipids will make the fluid domain shrink, relieving some interfacial energy. For more, see here and here
Melting dynamics of unilamellar vesicles. We have been working to understand the dynamics of vesicles subject to an ultrafast temperature jump that changes their phase, as studied in experiments by the Dyer group here at Emory. Images from Ph.D. student Lara Patel’s research are shown below. For more, see here (pdf) or here (link).
Rheology of telechelic hydrogels The mechanical properties of self-assembled transient networks are characterized by a relaxation time; roughly speaking, they behave solid-like over time periods shorter than this relaxation time and liquid-like over longer time periods. The stiffness of the solid-like behavior is described by a plateau shear modulus, which is sensitive to the degree of connectivity within the network. Through simulation and theory, group alumna Ana West uncovered an interesting relationship between the plateau shear modulus and the shear relaxation time in self-assembled transient networks. The model fits (some, not all) experimental data from the literature rather nicely. The results are described here.
Kindt Group on Youtube: Molecular animations as teaching tools